ARCH模型案例

发表于 | 更新于 | 分类于
条件异方差模型的一个案例

实例

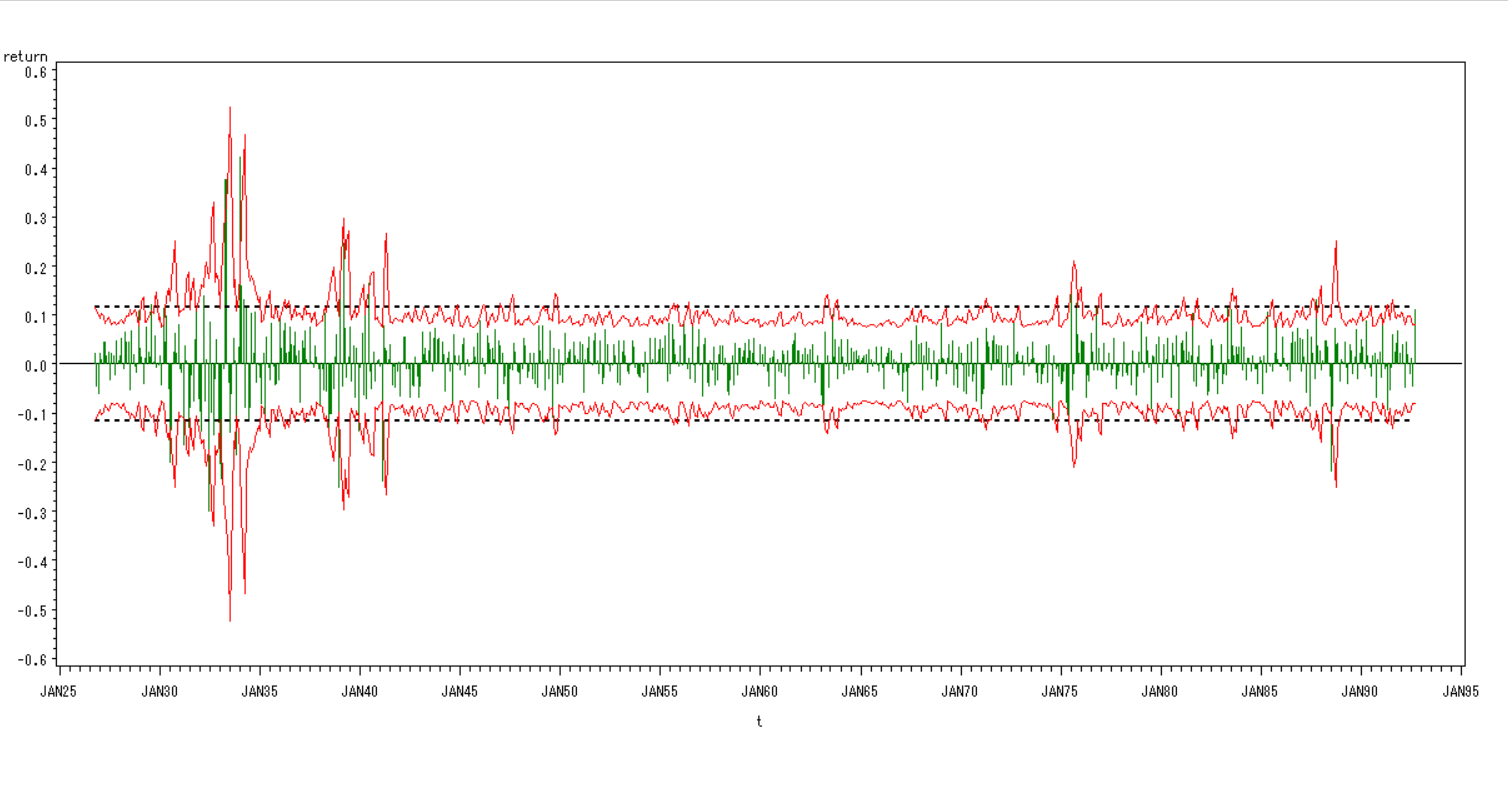
对1926-1991年标普500股票股价波动的模型拟合

数据录入

1
2
3
4
5
6
7
data a;
input return@@;
t=intnx('month','1oct1926'd,_n_-1);
format t monyy5.;
cards;
...  # 数据集
;

模型构建

ARIMA(尝试)

对原序列进行模型识别,尝试建立ARMA模型失败.由图,序列自相关系数落在两倍标准差之上,具有长期自相关的特征

1
2
proc arima;
identify var=return minic;

自相关图

序列总体定阶 q=3

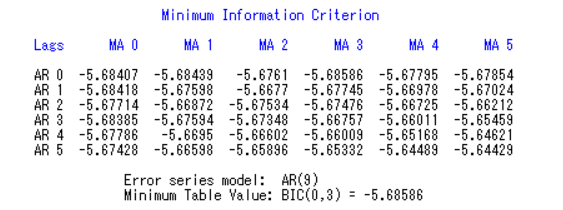
最小信息准则

残差自回归模型

1
2
3
4
5
6
7
8
9
proc autoreg;

# 指令系统建立序列return的线性回归模型,
#绘制残差序列的5阶自相关图,输出dw检验及P值,对残差序列进行异方差检验.
# garch=(q=3) noint 通过对输出的分析后加的
model return=t/nlag=5 dwprob archtest garch=(q=3) noint;

# 输出到out数据集中
output  out=out lcl=lcl ucl=ucl cev=cev;

DW检验显示与时间t不存在相关性

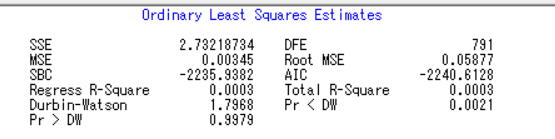
普通最小二乘估计输出结果

残差序列5阶滞后自相关图不存在截尾特征

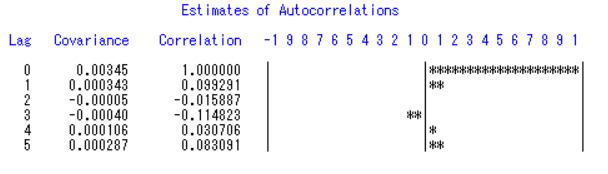
残差序列5阶滞后自相关图

异方差检验,拒绝原假设,方差非齐

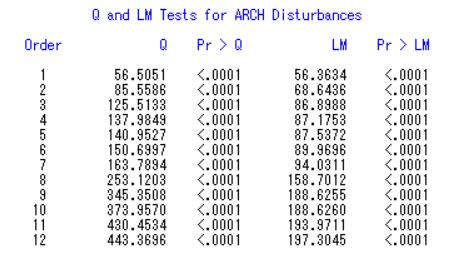
异方差检验结果

结合自相关图和异方差检验,拟合ARCH(3)模型

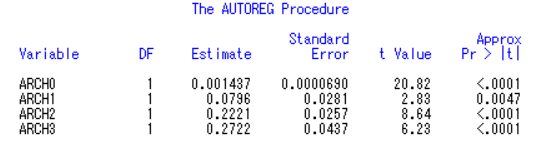
最终模型参数检验

拟合图形绘制

1
2
3
4
5
6
7
8
9
10
data out;
set out;
Lcl_ARCH=-1.96*sqrt(cev);
Ucl_ARCH=1.96*sqrt(cev);
proc gplot data=out;
plot return*t=2 lcl*t=3 LCL_arch*t=4 ucl*t=3 UCL_arch*t=4 /overlay;
symbol2 c=green i=needle v=none ;
symbol3 c=black i=join v=none w=2 l=2;
symbol4 c=red i=join v=none ;
run;

拟合图